UiRef
UiRef (User Input REsolution Framework) is an automated approach for resolving the semantics of user inputs requested by Android applications. To resolve these semantics, UiRef’s main tasks consist of layout extraction, label resolution, and semantics resolution. UiRef’s layout extraction instruments APKs to force the rendering of their layouts and exports the rendered layouts for further analysis. For label resolution, UiRef introduces a new algorithm to identify patterns within the placement and orientation of labels with respect to input widgets in the layout and geometrically resolves labels. UiRef’s semantics resolution applies text analytics techniques on the input widget’s associated text to determine the expected type of information accepted by the input widgets. Our WiSec 2017 paper describes UiRef in detail.
Source Code
The source code for UiRef is available on GitHub.
Extended Details
The following section provide extended details that were not included in the paper due to space constraints.
ROAD Algorithm for Outlier Detection
In this section, we describe UiRef’s approach for identifying anomalous input requests, as discussed in Secion 6.2 of our WiSec 2017 paper.
The goal of outlier analysis is to identify abnormal input requests that do not align with the purpose and functionality of the application. Since different types of applications vary in types of the information that they request, comparing sensitive input requests across a broad range of applications is not sufficient to identify outliers. For example, a financial application may be expected to request the user’s income while a game would not be expected to do so. Therefore, we perform outlier analysis at the granularity of Google Play’s 42 application categories. Note that we combine all of the 18 subcategories of games into a single “game” category, which results in 25 categories of applications.
To detect outliers for each Google Play category, we perform two tasks. First, we manually collapse sensitive concepts into 75 semantic buckets. For example, first name and last name are grouped in a person name bucket. The table below shows 5 of the 75 semantic buckets along with an excerpt of the associated terms. Second, we apply an unsupervised technique, called the Ranking-based Outlier Analysis and Detection (ROAD) algorithm, to generate a ranked list based on the likelihood that a record is an outlier.
|
|
|
|---|---|
| username or email addr | email address, email adress, email id, emailid, gmail address, screenname, username, ... |
| credit card info | credit card number, card number, card code, cvv code, cvv, cvc, credit card expiration, ... |
| person name | first name, middle name, last name, full name, middle initial, legal name, credit card holder, ... |
| phone number | phone number, telephone number, mobile phone, cell, work phone, home phone, fax number, ... |
| location info | city, town, state, zip, zip code, post code, street address, ship address, billing address, ... |
The ROAD algorithm was chosen over other outlier detection approaches multiple reasons. First, our dataset consists of categorical variables that are supported by the ROAD algorithm using k-modes with the dissimilarity function proposed by Ng et al.. In contrast, other popular approaches, such as One-class SVM and k-means, were designed for continuous variables. Second, we chose the ROAD algorithm instead of other common outlier detection approaches designed for categorical data, such as attribute value frequency (AVF), as the ROAD algorithm produces a multi-dimensional outlier ranking based on the dissimilarity of the data records from the largest clusters and the density of those clusters rather than the occurrence frequency of the attributes.</p>
To detect outliers, the ROAD algorithm operates in two phases. First, k-modes is applied to cluster the categorical data records to discover common trends (i.e., the largest-sized clusters). We choose the value of k by iteratively running k-modes to maximize the silhouette score, which is a metric that measures the similarity of a record to its own cluster compared to records in neighboring clusters.
The dissimilarity function, as shown below, is a modified version of the dissimilarity function proposed by Ng et al..
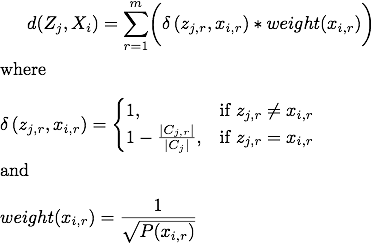
The distance function is defined as d(Zj,Xi),
where Zj is the mode of the jth cluster,
Cj, and Xi is the categorical data record.
The distance between Zj and Xi is the
summation of the dissimilarity scores for each of the m attributes in
the categorical data records. The dissimilarity score for the rth
attribute is 1 if the value of zj,r does not equal the
attribute value of xi,r, and 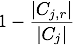 otherwise, where |Cj,r| is the
number of records in cluster Cj with the attribute value
xi,r, and |Cj| is the number of records in cluster
Cj.
otherwise, where |Cj,r| is the
number of records in cluster Cj with the attribute value
xi,r, and |Cj| is the number of records in cluster
Cj.
Note that we modify the distance function by multiplying the dissimilarity score by a probability-based value weighting function. We modify the weighting functions so that rare attribute values have a larger influence on the distance calculation. For example, if most applications do not request the user’s social security number (SSN), it is more significant that an application requests the user’s SSN than not requesting the user’s SSN. Therefore, the attribute value of requesting the user’s SSN (i.e., rare values) holds more weight in the distance function than the attribute value of not requesting the user’s SSN (i.e., frequent values). The weighting function, weight(xi,r), is the reciprocal of the square root of the probability that the value of xi,r occurs in the categorical dataset. The probability, P(xi,r), is the frequency of the value of xi,r divided by the total number of categorical data records. The weighting function returns a higher weight for rare occurrences of attribute values.
Second, the ROAD algorithm uses the resulting clusters to rank records by their distance from the largest-sized clusters and the density score of the record. A large cluster is defined as a cluster that has more than α% of the data records in the cluster. In our implementation of the ROAD algorithm, we initially set α to the experimentally determined value of 20% for each category, and decrement α by a half a percent until a large cluster is found. Note that we chose to start at 20%, as it ensured that smaller sized clusters were not accidentally included when choosing the large cluster. Further, we chose to decrement by a half percent until a large cluster is found, because it also ensures that only the largest clusters are chosen. To calculate the distance of each data record from the large clusters, we use the same modified dissimilarity function described above. The density score the summation of the probability that the value xi,r occurs divided by the number of attributes. The records are sorted in descending order based on the cluster distances, and in ascending order by the density score when the cluster distances between the two records are equal. A higher distance from the largest cluster denotes and a lower density score denotes that the record is more-likely an outlier.
Input Request Outliers Results
The following table shows the complete results of our outlier analysis, where k equals the number of clusters and the counts in parenthesis represent the number of applications.

Publications
- Benjamin Andow, Akhil Acharya, Dengfeng Li, William Enck, Kapil Singh, and Tao Xie, UiRef: Analysis of Sensitive User Inputs in Android Applications, in Proceedings of the ACM Conference on Security and Privacy in Wireless and Mobile Networks (WiSec), Jul. 2017.
[PDF] (acceptance rate=22.3%)
